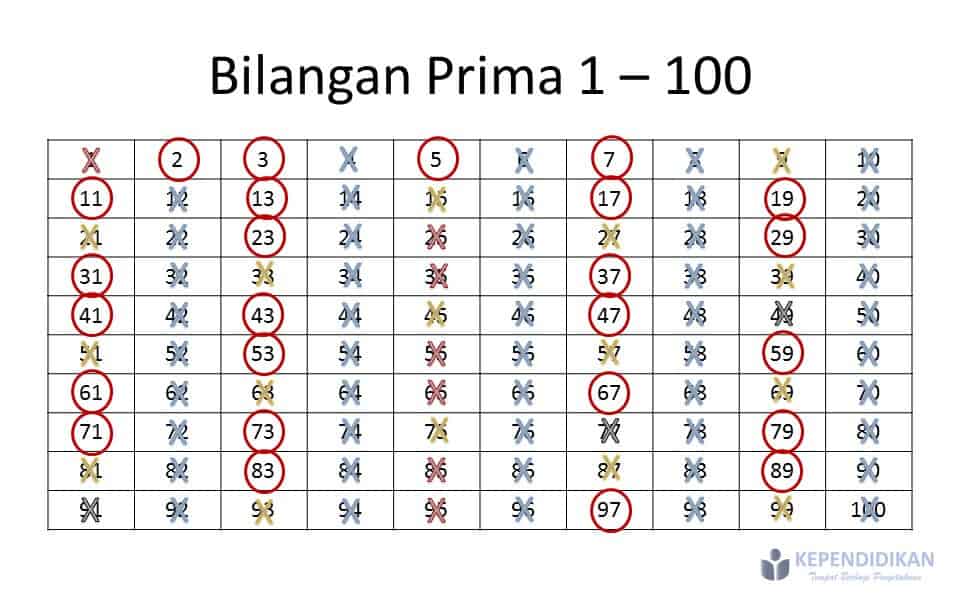
Mengungkap Rahasia Angka Ajaib: Bilangan Prima untuk Kelas 4 SD

Halo, Adik-adik calon matematikawan! Pernahkah kalian mendengar tentang "angka ajaib" atau "angka istimewa" dalam matematika? Hari ini, kita akan berkenalan dengan salah satu di antaranya, yaitu Bilangan Prima. Jangan khawatir, bilangan prima itu seru dan mudah dipahami, kok! Yuk, kita mulai petualangan kita di dunia angka!

Apa Itu Bilangan Prima? (Definisi Sederhana)

Bayangkan kalian punya sekumpulan permen. Jika kalian ingin membagi permen itu kepada teman-teman, ada beberapa cara, kan? Misalnya, jika punya 6 permen, kalian bisa membaginya ke 1 teman (dia dapat 6), 2 teman (masing-masing dapat 3), 3 teman (masing-masing dapat 2), atau 6 teman (masing-masing dapat 1). Angka 6 ini punya banyak cara pembagian.

Nah, bilangan prima itu angka yang "pemilih" banget dalam hal pembagian. Bilangan prima adalah bilangan asli yang hanya punya DUA faktor, yaitu angka 1 dan dirinya sendiri.

Bingung dengan kata "faktor"? Faktor adalah angka-angka yang bisa membagi habis suatu bilangan. Contohnya, faktor dari 6 adalah 1, 2, 3, dan 6.

Jadi, kalau bilangan prima, dia cuma bisa dibagi habis oleh dua angka saja: angka 1, dan angka itu sendiri. Tidak ada angka lain!

Ciri-Ciri Bilangan Prima

Agar lebih mudah mengingatnya, perhatikan ciri-ciri bilangan prima berikut:

1. Hanya Punya Dua Faktor: Ini adalah ciri utama dan terpenting. Misalnya, angka 7. Bisakah 7 dibagi habis oleh angka selain 1 dan 7? Tidak bisa! 7:1=7, 7:7=1. Tidak ada angka lain yang bisa membagi 7 tanpa sisa. Jadi, 7 adalah bilangan prima.
2. Angka 1 Bukan Bilangan Prima: Meskipun angka 1 hanya bisa dibagi oleh 1 (dirinya sendiri), dia hanya punya SATU faktor, bukan DUA. Ingat, bilangan prima harus punya DUA faktor. Jadi, angka 1 bukan bilangan prima, dan juga bukan bilangan komposit (lawan dari prima). Angka 1 itu spesial!
3. Angka 2 Adalah Bilangan Prima Terkecil dan Satu-satunya yang Genap: Ini juga sangat penting! Angka 2 adalah satu-satunya bilangan prima yang genap. Kenapa? Karena semua bilangan genap lainnya (4, 6, 8, 10, dst.) pasti bisa dibagi 2. Kalau bisa dibagi 2, berarti faktornya sudah lebih dari dua (yaitu 1, 2, dan dirinya sendiri). Contoh: 4 punya faktor 1, 2, 4. Jadi 4 bukan prima.

Bagaimana Cara Menemukan Bilangan Prima? (Mencari Faktor)

Cara paling mudah untuk menemukan apakah suatu bilangan itu prima atau bukan adalah dengan mencoba mencari faktor-faktornya. Mari kita coba dari angka-angka kecil:

• Angka 1: Faktornya hanya 1. (Bukan prima, karena cuma 1 faktor).
• Angka 2: Faktornya 1 dan 2. (Prima! Karena punya 2 faktor).
• Angka 3: Faktornya 1 dan 3. (Prima! Karena punya 2 faktor).
• Angka 4: Faktornya 1, 2, dan 4. (Bukan prima! Karena punya 3 faktor).
• Angka 5: Faktornya 1 dan 5. (Prima! Karena punya 2 faktor).
• Angka 6: Faktornya 1, 2, 3, dan 6. (Bukan prima! Karena punya 4 faktor).
• Angka 7: Faktornya 1 dan 7. (Prima! Karena punya 2 faktor).
• Angka 8: Faktornya 1, 2, 4, dan 8. (Bukan prima!).
• Angka 9: Faktornya 1, 3, dan 9. (Bukan prima!).
• Angka 10: Faktornya 1, 2, 5, dan 10. (Bukan prima!).

Lihat, mudah kan? Kita hanya perlu mencoba membagi angka tersebut dengan angka-angka yang lebih kecil dari dirinya (mulai dari 2, 3, 4, dan seterusnya). Jika ada yang bisa membagi habis selain 1 dan dirinya sendiri, berarti dia bukan prima.

Mengapa Bilangan Prima Itu Penting?

Mungkin kalian bertanya, "Untuk apa sih kita belajar bilangan prima ini?" Bilangan prima itu seperti "batu bata" atau "blok bangunan" dasar dari semua bilangan asli lainnya. Setiap bilangan asli yang lebih besar dari 1 bisa dibuat dari perkalian bilangan-bilangan prima. Konsep ini sangat penting di matematika yang lebih tinggi, bahkan digunakan dalam kode rahasia di komputer (kriptografi)! Jadi, ini adalah fondasi yang keren untuk dipelajari.

Contoh Soal Matematika Bilangan Prima Kelas 4 SD

Sekarang, mari kita latih pemahaman kita dengan beberapa contoh soal. Ingat, jangan takut salah, yang penting berani mencoba!

Tipe Soal 1: Mengidentifikasi Bilangan Prima

Soal 1:
Apakah angka 11 adalah bilangan prima? Jelaskan jawabanmu!

Pembahasan:
Untuk menentukan apakah 11 adalah bilangan prima, kita harus mencari faktor-faktornya.

• Apakah 11 bisa dibagi 1? Ya, 11 : 1 = 11. (Faktor: 1)
• Apakah 11 bisa dibagi 2? Tidak, 11 : 2 = 5 sisa 1.
• Apakah 11 bisa dibagi 3? Tidak, 11 : 3 = 3 sisa 2.
• Apakah 11 bisa dibagi 4? Tidak, 11 : 4 = 2 sisa 3.
• Apakah 11 bisa dibagi 5? Tidak, 11 : 5 = 2 sisa 1.
• Apakah 11 bisa dibagi 6? Tidak, 11 : 6 = 1 sisa 5.
• Apakah 11 bisa dibagi 7? Tidak, 11 : 7 = 1 sisa 4.
• Apakah 11 bisa dibagi 8? Tidak, 11 : 8 = 1 sisa 3.
• Apakah 11 bisa dibagi 9? Tidak, 11 : 9 = 1 sisa 2.
• Apakah 11 bisa dibagi 10? Tidak, 11 : 10 = 1 sisa 1.
• Apakah 11 bisa dibagi 11? Ya, 11 : 11 = 1. (Faktor: 11)

Kita menemukan bahwa angka 11 hanya memiliki dua faktor, yaitu 1 dan 11.
Jadi, ya, 11 adalah bilangan prima.

Soal 2:
Apakah angka 15 adalah bilangan prima? Jelaskan jawabanmu!

Pembahasan:
Kita cari faktor-faktor dari 15.

• Apakah 15 bisa dibagi 1? Ya, 15 : 1 = 15. (Faktor: 1)
• Apakah 15 bisa dibagi 2? Tidak, 15 : 2 = 7 sisa 1.
• Apakah 15 bisa dibagi 3? Ya, 15 : 3 = 5. (Faktor: 3)
• Karena 15 bisa dibagi 3 (selain 1 dan 15), kita sudah tahu bahwa 15 memiliki lebih dari dua faktor (yaitu 1, 3, 5, dan 15).
  Jadi, tidak, 15 BUKAN bilangan prima. (15 adalah bilangan komposit).

Soal 3:
Perhatikan daftar angka berikut: 2, 4, 7, 9, 13. Lingkari semua bilangan prima dari daftar tersebut!

Pembahasan:
Mari kita periksa satu per satu:

• 2: Faktornya 1 dan 2. (Prima!)
• 4: Faktornya 1, 2, dan 4. (Bukan prima!)
• 7: Faktornya 1 dan 7. (Prima!)
• 9: Faktornya 1, 3, dan 9. (Bukan prima!)
• 13: Kita coba bagi 13 dengan angka-angka yang lebih kecil:
  • 13 : 2 = 6 sisa 1
  • 13 : 3 = 4 sisa 1
  • 13 : 4 = 3 sisa 1
  • 13 : 5 = 2 sisa 3
  • 13 : 6 = 2 sisa 1
  • Hanya bisa dibagi 1 dan 13. (Prima!)

Jadi, bilangan prima dari daftar tersebut adalah: 2, 7, 13.

Tipe Soal 2: Menentukan Bilangan Prima dalam Rentang Tertentu

Soal 4:
Daftarkan semua bilangan prima yang terletak di antara angka 20 dan 30!

Pembahasan:
Kita akan memeriksa setiap angka dari 21 sampai 29.

• 21: Bisa dibagi 3 (21:3=7) dan 7 (21:7=3). Bukan prima.
• 22: Bisa dibagi 2 (22:2=11). Bukan prima.
• 23: Mari kita coba bagi:
  • 23 : 2 = sisa
  • 23 : 3 = sisa
  • 23 : 4 = sisa
  • 23 : 5 = sisa
  • … hanya bisa dibagi 1 dan 23. (Prima!)
• 24: Bisa dibagi 2, 3, 4, 6, 8, 12. Bukan prima.
• 25: Bisa dibagi 5 (25:5=5). Bukan prima.
• 26: Bisa dibagi 2 (26:2=13). Bukan prima.
• 27: Bisa dibagi 3 (27:3=9) dan 9 (27:9=3). Bukan prima.
• 28: Bisa dibagi 2, 4, 7, 14. Bukan prima.
• 29: Mari kita coba bagi:
  • 29 : 2 = sisa
  • 29 : 3 = sisa
  • 29 : 4 = sisa
  • 29 : 5 = sisa
  • … hanya bisa dibagi 1 dan 29. (Prima!)

Jadi, bilangan prima di antara 20 dan 30 adalah 23 dan 29.

Soal 5:
Tentukan bilangan prima terbesar yang kurang dari 50!

Pembahasan:
Kita perlu mencari angka prima yang paling dekat dengan 50, tetapi masih di bawah 50. Mari kita coba dari 49, lalu mundur.

• 49: Bisa dibagi 7 (49:7=7). Bukan prima.
• 48: Bisa dibagi 2, 3, 4, 6, 8, 12, 16, 24. Bukan prima.
• 47: Mari kita coba bagi 47 dengan angka-angka kecil:
  • 47 : 2 = sisa
  • 47 : 3 = sisa
  • 47 : 4 = sisa
  • 47 : 5 = sisa
  • 47 : 6 = sisa
  • 47 : 7 = sisa (47 = 6×7 + 5)
  • … Sepertinya hanya bisa dibagi 1 dan 47. (Prima!)

Karena 47 adalah bilangan prima dan semua angka setelahnya hingga 50 (48, 49) bukan prima, maka 47 adalah yang terbesar.
Jadi, bilangan prima terbesar yang kurang dari 50 adalah 47.

Tipe Soal 3: Melengkapi Pernyataan

Soal 6:
Lengkapi pernyataan berikut:
a. Bilangan prima terkecil adalah .
b. Satu-satunya bilangan prima yang genap adalah .
c. Bilangan asli yang hanya memiliki satu faktor (bukan prima dan bukan komposit) adalah ____.

Pembahasan:
a. Kita sudah belajar bahwa 2 adalah bilangan prima pertama dan terkecil.
b. Kita juga tahu bahwa 2 adalah satu-satunya bilangan prima yang genap, karena semua bilangan genap lainnya pasti bisa dibagi 2.
c. Angka 1 adalah angka yang spesial, dia hanya punya satu faktor yaitu 1. Oleh karena itu, dia bukan prima dan bukan komposit.

Jawaban:
a. Bilangan prima terkecil adalah 2.
b. Satu-satunya bilangan prima yang genap adalah 2.
c. Bilangan asli yang hanya memiliki satu faktor (bukan prima dan bukan komposit) adalah 1.

Tipe Soal 4: Soal Cerita Sederhana

Soal 7:
Pak Budi memiliki 19 butir kelereng. Ia ingin membagikan kelereng tersebut kepada beberapa anaknya secara merata, tanpa ada sisa. Jika Pak Budi memiliki lebih dari satu anak, apakah ia bisa membagikan kelereng tersebut secara merata? Jelaskan!

Pembahasan:
Untuk menjawab soal ini, kita perlu tahu apakah 19 adalah bilangan prima atau bukan.

• Kita cari faktor dari 19.
• 19 hanya bisa dibagi 1 dan 19. Tidak ada angka lain yang bisa membagi 19 tanpa sisa.
• Ini berarti 19 adalah bilangan prima.

Jika 19 adalah bilangan prima, itu artinya Pak Budi hanya bisa membagi kelereng secara merata kepada:

1. 1 orang anak (anak tersebut akan mendapat 19 kelereng).
2. 19 orang anak (masing-masing anak akan mendapat 1 kelereng).

Soal ini bertanya apakah ia bisa membagikan kelereng secara merata jika ia memiliki lebih dari satu anak. Jika ia punya 2, 3, 4, atau lebih anak (tapi kurang dari 19), kelerengnya tidak akan bisa dibagi rata tanpa sisa.

Jawaban:
Tidak, Pak Budi tidak bisa membagikan 19 butir kelereng secara merata kepada lebih dari satu anaknya (selain 19 anak) tanpa sisa. Ini karena 19 adalah bilangan prima, yang berarti faktornya hanya 1 dan 19. Jadi, pembagian rata hanya mungkin jika anaknya 1 atau 19.

Soal 8:
Siti memiliki 29 buah jeruk. Dia ingin memasukkan jeruk-jeruk itu ke dalam beberapa keranjang. Setiap keranjang harus berisi jumlah jeruk yang sama, dan tidak boleh ada jeruk yang tersisa. Berapa banyak cara Siti bisa memasukkan jeruk-jeruk itu ke dalam keranjang, jika jumlah keranjangnya harus lebih dari satu?

Pembahasan:
Sama seperti soal sebelumnya, kita harus mencari tahu apakah 29 adalah bilangan prima.

• Kita cari faktor dari 29.
• Setelah kita coba bagi dengan angka-angka kecil (2, 3, 4, 5, dst.), kita akan menemukan bahwa 29 hanya bisa dibagi 1 dan 29.
• Ini berarti 29 adalah bilangan prima.

Jika 29 adalah bilangan prima, maka hanya ada dua cara untuk membagi jeruk secara merata:

1. Memasukkan semua 29 jeruk ke dalam 1 keranjang.
2. Memasukkan 1 jeruk ke dalam 29 keranjang.

Soal ini meminta cara jika jumlah keranjangnya lebih dari satu.

Jawaban:
Siti hanya memiliki satu cara untuk memasukkan jeruk ke dalam keranjang jika jumlah keranjangnya lebih dari satu, yaitu dengan menggunakan 29 keranjang (masing-masing berisi 1 jeruk). Jika jumlah keranjang bukan 1 atau 29, maka jeruk tidak akan bisa dibagi rata karena 29 adalah bilangan prima.

Tips Sukses Belajar Bilangan Prima

• Pahami Konsep "Dua Faktor": Ini adalah kunci utamanya. Selalu ingat bahwa bilangan prima hanya punya faktor 1 dan dirinya sendiri.
• Hafalkan Bilangan Prima Kecil: Cobalah hafalkan bilangan prima di bawah 20: 2, 3, 5, 7, 11, 13, 17, 19. Ini akan sangat membantu!
• Latihan Mencari Faktor: Sering-seringlah berlatih mencari faktor dari suatu bilangan. Ini akan membuat kalian lebih cepat menentukan apakah suatu bilangan itu prima atau bukan.
• Jangan Takut Salah: Matematika itu tentang mencoba dan belajar dari kesalahan. Teruslah berlatih!

Penutup

Wah, tidak terasa kita sudah belajar banyak tentang bilangan prima! Dari definisi sederhana, ciri-ciri uniknya, cara menemukannya, hingga menyelesaikan berbagai contoh soal. Bilangan prima memang angka yang istimewa dan memiliki peran penting dalam dunia matematika.

Teruslah berlatih dan jangan pernah berhenti bertanya, ya! Siapa tahu, suatu hari nanti kalian bisa menemukan rahasia-rahasia baru tentang bilangan prima yang belum terungkap! Selamat belajar dan berpetualang di dunia angka!