Segi banyak, sebuah konsep fundamental dalam geometri, menjadi salah satu materi penting yang dipelajari siswa kelas 4 Sekolah Dasar pada semester kedua. Memahami apa itu segi banyak, bagaimana mengidentifikasinya, serta mengenal jenis-jenisnya adalah kunci untuk membangun dasar matematika yang kuat. Latihan soal yang variatif dan pembahasan yang mendalam akan membantu siswa tidak hanya menghafal, tetapi benar-benar memahami konsep ini. Artikel ini akan menyajikan kumpulan latihan soal beserta pembahasan rinci, dirancang khusus untuk siswa kelas 4 SD semester 2, dengan tujuan menguasai materi segi banyak.

Apa Itu Segi Banyak? Memahami Konsep Dasar

Sebelum kita melangkah ke latihan soal, mari kita segarkan kembali ingatan kita tentang apa itu segi banyak. Segi banyak adalah bangun datar tertutup yang dibatasi oleh garis-garis lurus. Kata "segi" merujuk pada sisi, dan "banyak" berarti lebih dari dua. Jadi, secara sederhana, segi banyak adalah bangun datar yang memiliki banyak sisi.

Beberapa karakteristik penting dari segi banyak meliputi:

• Tertutup: Garis-garis pembatasnya bertemu dan membentuk sebuah area yang tertutup. Tidak ada celah atau bukaan.
• Dibatasi Garis Lurus: Sisi-sisi segi banyak harus berupa segmen garis lurus. Tidak ada sisi yang melengkung.
• Memiliki Sudut: Pertemuan dua sisi pada titik disebut sudut. Setiap segi banyak memiliki jumlah sudut yang sama dengan jumlah sisinya.
• Memiliki Titik Sudut: Titik tempat dua sisi bertemu disebut titik sudut.

Jenis-Jenis Segi Banyak: Dari yang Sederhana Hingga Kompleks

Segi banyak diklasifikasikan berdasarkan jumlah sisinya. Semakin banyak sisinya, semakin kompleks bentuknya. Berikut adalah beberapa jenis segi banyak yang umum dipelajari di kelas 4 SD:

1. Segitiga: Segi banyak dengan 3 sisi dan 3 sudut. Contohnya segitiga sama sisi, segitiga sama kaki, segitiga siku-siku.
2. Segi Empat (Persegi Panjang, Persegi, Jajar Genjang, Trapesium, Belah Ketupat, Layang-layang): Segi banyak dengan 4 sisi dan 4 sudut.
3. Segi Lima (Pentagon): Segi banyak dengan 5 sisi dan 5 sudut.
4. Segi Enam (Heksagon): Segi banyak dengan 6 sisi dan 6 sudut.
5. Segi Tujuh (Heptagon): Segi banyak dengan 7 sisi dan 7 sudut.
6. Segi Delapan (Oktagon): Segi banyak dengan 8 sisi dan 8 sudut.

Selain itu, segi banyak dapat dibedakan menjadi:

• Segi Banyak Beraturan: Segi banyak yang semua sisinya sama panjang dan semua sudutnya sama besar. Contohnya persegi, segitiga sama sisi, segi enam beraturan.
• Segi Banyak Tidak Beraturan: Segi banyak yang sisi-sisinya tidak sama panjang atau sudut-sudutnya tidak sama besar, atau keduanya. Contohnya segitiga sembarang, persegi panjang.

Mengapa Latihan Soal Penting?

Latihan soal adalah jembatan antara pemahaman teori dan kemampuan aplikasi. Dengan mengerjakan berbagai jenis soal, siswa dapat:

• Memperkuat Pemahaman: Mengaplikasikan konsep yang telah dipelajari dalam situasi yang berbeda.
• Mengidentifikasi Kesulitan: Mengetahui bagian mana dari materi yang masih perlu diperdalam.
• Meningkatkan Keterampilan: Melatih kemampuan berpikir logis, analisis, dan pemecahan masalah.
• Membangun Kepercayaan Diri: Semakin banyak berlatih dan berhasil, semakin percaya diri siswa dalam menghadapi soal-soal matematika.

Mari kita mulai latihan soalnya!

Latihan Soal Segi Banyak Kelas 4 SD Semester 2

Soal 1: Identifikasi Segi Banyak

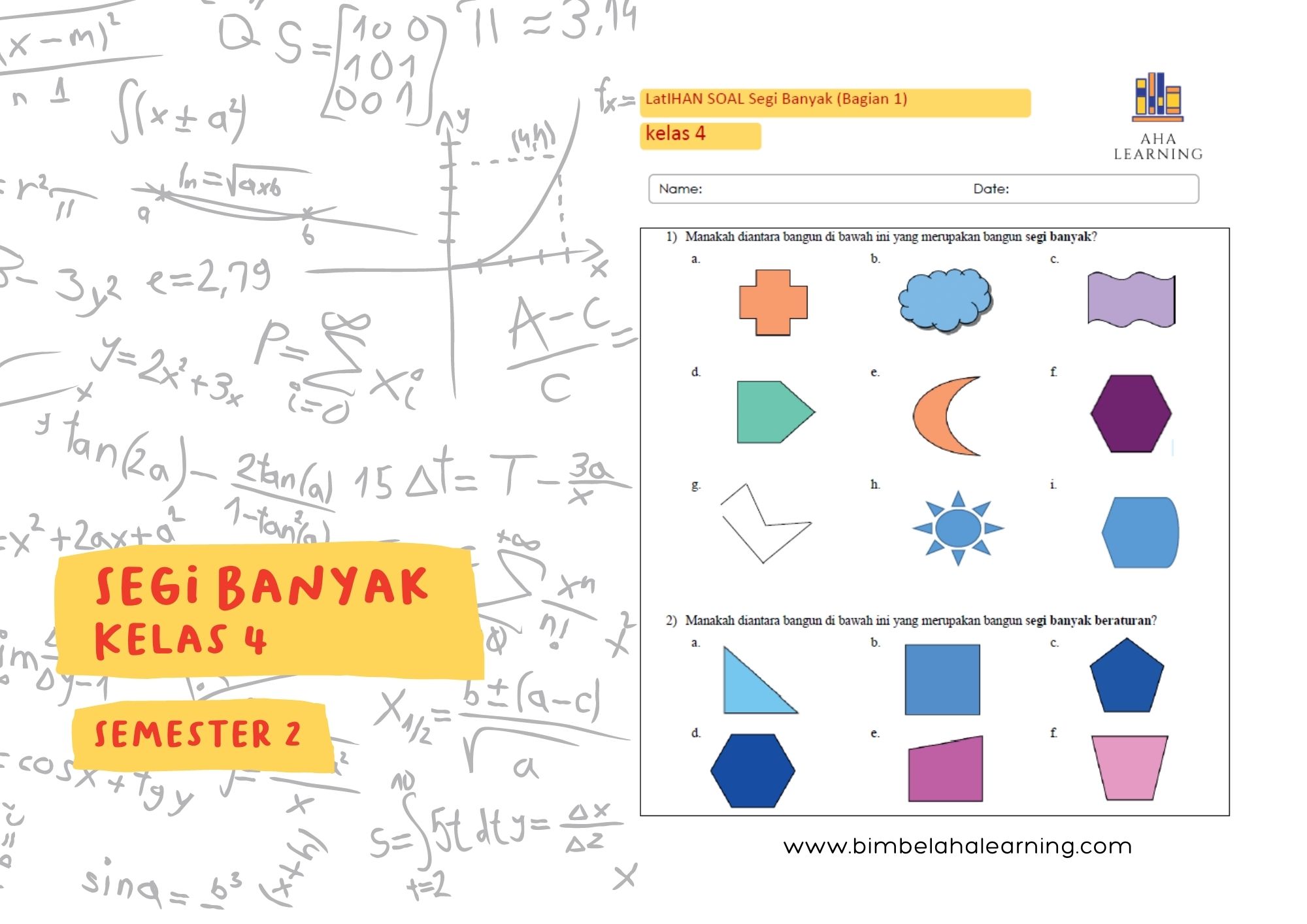
Perhatikan gambar-gambar berikut. Lingkarilah gambar yang merupakan segi banyak!

(Guru dapat menyajikan gambar-gambar seperti: lingkaran, persegi, segitiga, oval, persegi panjang, bintang (yang sisinya lurus dan tertutup), trapesium, huruf ‘U’ terbuka, dan bentuk lain yang tidak beraturan namun tetap segi banyak.)

Pembahasan Soal 1:

Untuk menentukan apakah sebuah gambar adalah segi banyak, kita perlu memeriksa dua syarat utama: tertip dan dibatasi oleh garis-garis lurus.

• Lingkaran: Bukan segi banyak karena dibatasi oleh garis lengkung.
• Persegi: Adalah segi banyak karena tertutup dan dibatasi oleh 4 garis lurus.
• Segitiga: Adalah segi banyak karena tertutup dan dibatasi oleh 3 garis lurus.
• Oval: Bukan segi banyak karena dibatasi oleh garis lengkung.
• Persegi Panjang: Adalah segi banyak karena tertutup dan dibatasi oleh 4 garis lurus.
• Bintang (yang sisinya lurus dan tertutup): Adalah segi banyak karena tertutup dan dibatasi oleh garis-garis lurus.
• Trapesium: Adalah segi banyak karena tertutup dan dibatasi oleh 4 garis lurus.
• Huruf ‘U’ terbuka: Bukan segi banyak karena tidak tertutup.
• Bentuk tidak beraturan (namun tetap segi banyak): Jika tertutup dan hanya dibatasi garis lurus, maka itu adalah segi banyak.

Soal 2: Menghitung Jumlah Sisi dan Sudut

Sebutkan jumlah sisi dan jumlah sudut dari segi banyak berikut:

a. Segi Lima
b. Segi Delapan
c. Segitiga
d. Segi Enam

Pembahasan Soal 2:

Jumlah sisi dan jumlah sudut pada sebuah segi banyak selalu sama.

a. Segi Lima: Memiliki 5 sisi dan 5 sudut. Nama lainnya adalah Pentagon.
b. Segi Delapan: Memiliki 8 sisi dan 8 sudut. Nama lainnya adalah Oktagon.
c. Segitiga: Memiliki 3 sisi dan 3 sudut.
d. Segi Enam: Memiliki 6 sisi dan 6 sudut. Nama lainnya adalah Heksagon.

Soal 3: Mengidentifikasi Segi Banyak Beraturan dan Tidak Beraturan

Perhatikan gambar-gambar berikut. Beri tanda centang (✓) pada kolom yang sesuai.

Gambar	Nama Segi Banyak	Beraturan	Tidak Beraturan
(Gambar persegi)	Persegi
(Gambar segitiga sama sisi)	Segitiga
(Gambar persegi panjang)	Persegi Panjang
(Gambar segitiga sembarang)	Segitiga
(Gambar segi enam beraturan)	Segi Enam

Pembahasan Soal 3:

Ingat kembali definisi segi banyak beraturan: semua sisinya sama panjang dan semua sudutnya sama besar.

• Persegi: Semua sisinya sama panjang dan semua sudutnya siku-siku (sama besar). Jadi, Beraturan.
• Segitiga sama sisi: Semua sisinya sama panjang dan semua sudutnya sama besar (masing-masing 60 derajat). Jadi, Beraturan.
• Persegi panjang: Sisinya yang berhadapan sama panjang (tetapi sisi yang berdekatan bisa berbeda panjangnya). Semua sudutnya siku-siku (sama besar). Jika panjang dan lebarnya sama, maka ia menjadi persegi dan beraturan. Namun, secara umum, persegi panjang tidak selalu beraturan (kecuali jika ia adalah persegi). Dalam konteks ini, jika gambarnya persegi panjang biasa (bukan persegi), maka kita anggap Tidak Beraturan.
• Segitiga sembarang: Sisi-sisinya tidak sama panjang dan sudut-sudutnya tidak sama besar. Jadi, Tidak Beraturan.
• Segi enam beraturan: Sesuai namanya, semua sisinya sama panjang dan semua sudutnya sama besar. Jadi, Beraturan.

Soal 4: Menentukan Nama Segi Banyak Berdasarkan Sisi

Tuliskan nama segi banyak yang memiliki jumlah sisi sebagai berikut:

a. 5 sisi
b. 4 sisi
c. 7 sisi
d. 3 sisi
e. 6 sisi

Pembahasan Soal 4:

Ini adalah soal penguatan hafalan nama-nama segi banyak berdasarkan jumlah sisinya.

a. 5 sisi: Segi Lima (Pentagon)
b. 4 sisi: Segi Empat (Contohnya persegi, persegi panjang, jajar genjang, trapesium, belah ketupat, layang-layang)
c. 7 sisi: Segi Tujuh (Heptagon)
d. 3 sisi: Segitiga
e. 6 sisi: Segi Enam (Heksagon)

Soal 5: Mengelompokkan Bangun Datar

Kelompokkan bangun-bangun datar berikut ke dalam kategori "Segi Banyak" atau "Bukan Segi Banyak".

1. Lingkaran
2. Persegi
3. Trapesium
4. Bintang (dengan sisi lurus)
5. Setengah lingkaran
6. Segi Delapan
7. Jajar Genjang
8. Bentuk hati (yang sisinya melengkung)

Pembahasan Soal 5:

Kita kembali menggunakan kriteria utama: tertutup dan dibatasi garis lurus.

• Segi Banyak:

  • Persegi (tertutup, garis lurus)
  • Trapesium (tertutup, garis lurus)
  • Bintang (dengan sisi lurus) (tertutup, garis lurus)
  • Segi Delapan (tertutup, garis lurus)
  • Jajar Genjang (tertutup, garis lurus)

• Bukan Segi Banyak:

  • Lingkaran (garis lengkung)
  • Setengah lingkaran (tidak tertutup, ada garis lengkung)
  • Bentuk hati (dengan sisinya melengkung) (garis lengkung)

Soal 6: Menggambar Segi Banyak

Gambarlah contoh dari segi banyak berikut:

a. Segitiga Sama Kaki
b. Persegi
c. Segi Lima Beraturan (bisa digambar secara kasar)
d. Trapesium Siku-siku

Pembahasan Soal 6:

Soal ini bertujuan untuk melatih kemampuan visualisasi dan menggambar siswa.

a. Segitiga Sama Kaki: Memiliki dua sisi yang sama panjang dan dua sudut alas yang sama besar. Kaki-kakinya bertemu di satu titik.
b. Persegi: Bangun datar dengan empat sisi yang sama panjang dan empat sudut siku-siku.
c. Segi Lima Beraturan: Bangun datar dengan lima sisi yang sama panjang dan lima sudut yang sama besar. Bentuknya seperti rumah dengan atap lancip.
d. Trapesium Siku-siku: Trapesium yang memiliki dua sudut siku-siku. Salah satu sisi tegaknya tegak lurus dengan kedua sisi sejajarnya.

Soal 7: Mencari Segi Banyak dalam Kehidupan Sehari-hari

Carilah minimal tiga contoh benda di sekitarmu yang memiliki bentuk segi banyak. Sebutkan nama segi banyak tersebut.

Pembahasan Soal 7:

Soal ini mengajak siswa untuk melihat aplikasi konsep segi banyak di dunia nyata. Jawaban bisa bervariasi, namun contohnya bisa seperti:

• Ubin lantai: Bisa berbentuk persegi atau segi enam (heksagon).
• Buku: Biasanya berbentuk persegi panjang.
• Rambu lalu lintas: Beberapa rambu berbentuk segi delapan (misalnya rambu berhenti).
• Pizza yang dipotong: Potongan pizza seringkali berbentuk segitiga.
• Kotak makan siang: Bisa berbentuk persegi panjang atau persegi.
• Kertas origami: Seringkali dimulai dari kertas persegi.

Soal 8: Tantangan Segi Banyak

Budi menggambar sebuah segi banyak. Segi banyak tersebut memiliki 7 sisi.
a. Berapa jumlah sudut segi banyak yang digambar Budi?
b. Apakah segi banyak tersebut beraturan atau tidak beraturan? Jelaskan alasanmu! (Asumsi: jika tidak ada keterangan khusus, kita anggap sembarang).

Pembahasan Soal 8:

a. Jumlah sisi dan jumlah sudut pada segi banyak selalu sama. Jika segi banyak tersebut memiliki 7 sisi, maka ia juga memiliki 7 sudut.
b. Segi banyak yang digambar Budi adalah segi tujuh. Jika tidak ada keterangan lebih lanjut bahwa semua sisinya sama panjang dan semua sudutnya sama besar, maka kita bisa menganggapnya sebagai segi banyak tidak beraturan. Alasannya adalah karena ciri-ciri segi banyak beraturan adalah semua sisi sama panjang dan semua sudut sama besar. Jika salah satu atau kedua ciri tersebut tidak terpenuhi, maka segi banyak tersebut dianggap tidak beraturan.

Soal 9: Mengidentifikasi Pola

Perhatikan pola berikut:

Segitiga (3 sisi) -> Segi Empat (4 sisi) -> Segi Lima (5 sisi) -> …

a. Bentuk segi banyak selanjutnya dalam pola ini adalah …
b. Berapa jumlah sisi bentuk segi banyak selanjutnya?

Pembahasan Soal 9:

Pola ini menunjukkan penambahan satu sisi pada setiap langkah.

a. Jika kita melanjutkan pola tersebut, setelah segi lima (5 sisi), maka bentuk segi banyak selanjutnya adalah Segi Enam.
b. Segi enam memiliki 6 sisi.

Soal 10: Soal Cerita

Seorang tukang kebun ingin membuat pagar di taman berbentuk segi enam beraturan. Jika panjang satu sisi pagar adalah 2 meter, berapakah total panjang pagar yang dibutuhkan?

Pembahasan Soal 10:

Soal ini sedikit melatih konsep keliling, namun tetap terkait dengan segi banyak.

• Taman berbentuk segi enam beraturan. Segi enam memiliki 6 sisi.
• Panjang satu sisi pagar adalah 2 meter.
• Karena segi enam beraturan, maka semua sisinya memiliki panjang yang sama.
• Untuk mencari total panjang pagar, kita perlu menjumlahkan panjang semua sisinya, atau mengalikan panjang satu sisi dengan jumlah sisinya.
• Total panjang pagar = jumlah sisi × panjang satu sisi
• Total panjang pagar = 6 × 2 meter
• Total panjang pagar = 12 meter

Tips Tambahan untuk Siswa:

• Gunakan Benda Nyata: Cari benda-benda di rumah yang berbentuk segi banyak untuk memudahkan pemahaman.
• Gambar Berulang Kali: Latihlah kemampuan menggambar Anda dengan menggambar berbagai jenis segi banyak.
• Buat Kartu Hafalan: Buat kartu yang berisi gambar segi banyak, namanya, jumlah sisi, dan jumlah sudutnya.
• Berdiskusi: Diskusikan soal-soal yang sulit dengan teman atau guru.
• Jangan Takut Salah: Kesalahan adalah bagian dari proses belajar. Yang terpenting adalah mencoba dan memahami di mana letak kesalahannya.

Penutup

Menguasai konsep segi banyak adalah langkah awal yang penting dalam mempelajari geometri. Dengan latihan soal yang konsisten dan pemahaman yang mendalam terhadap setiap konsep, siswa kelas 4 SD semester 2 dapat membangun fondasi matematika yang kokoh. Teruslah berlatih, bertanya, dan jangan pernah berhenti belajar! Semoga artikel ini bermanfaat dalam perjalanan belajar Anda.